MATLAB的名称源自
Matrix Laboratory,它是一种科学计算软件,专门以矩阵的形式处理数据。
大二测绘系开设过matlab课程,除了认真上过第一节课,就再也没学了,哪怕是最后的期末作业,都是抄的。当然也就完全体会不到matlab的用处,对它的认识仅仅停留在“matlab”的六个字母上。三年后(2019-9-19),体验了下数学建模,负责编程任务,又重新学习了一下matlab的基本语法。
基本操作
clear y 将变量y从变量空间中去掉
clear 将所有变量清空
clc 仅仅是清空屏幕
% 注释
ctrl+R 批量注释
ctrl+T 批量取消注释
disp():屏幕打印
input():输入函数
strcat():合并字符串
num2str():数字->字符串
linspace(0,2,5) 产生从0到2的均匀的5个点
zeros(2,3) 初始化2行3列全为0的矩阵
ones(2) 初始化全为1的2阶的矩阵
eye(2) 初始化2阶单位阵
Inf 无穷大
F = A.*B 点乘,对应位置相乘,区别于矩阵乘法
F = A./B 点除,对应位置相除
F = A/B = A * B^-1 ,就是A*B的逆
F = A^2 = A*A
F = A.^2 = A.*A
x = A(1,3) 取A矩阵的第1行3列
y = A(2,:) 相当于 y = A(2,1:3) 取第二行
Z = A(1:2,1:3) 前2行前3列
A([2,5],:) 只取第2和第5行
10👎1 从10到1,公差为-1
A(2:end,:) 取第2行到最后一行
A(2:end-1,:) 取第2行到倒数第2行
A(:) 取全部元素,输出的是一个列向量
A(1,3) = 0 将0赋值给1行3列
A(2,:) = [6 5 4] 整行的赋值
size():求矩阵的大小,几行几列
[r,c] = size(A) 将A的行、列数分别赋值给r、c
r = size(A,1) 只返回行数
c = size(A,2) 只返回列数
B = repmat(A,m,n) 将A复制m*n块
inv(B) 求B的逆矩阵
prod(A) 按列相乘
prod(A,2) 按行相乘
E = eig(A) A的全部特征值,组成向量E
[V,D] = eig(A) A的全部特征值,构成对角阵D,且A的特征值构成V的列向量
比较和逻辑运算
>> x = [1 2 3 4 5 6 7 8 9];
>> y = [1 4 3 8 6 5 7 2 9];
>> eq = (x==y)
eq =
1×9 logical 数组
1 0 1 0 0 0 1 0 1
>> xy = (x>5)&(y<7)
xy =
1×9 logical 数组
0 0 0 0 0 1 0 1 0
>> xoy = (x>5)|(y<7)
xoy =
1×9 logical 数组
1 1 1 0 1 1 1 1 1
% 把x里小于0的都改为0,省的写for循环
>> x = [1 -2 3 -4 5 -6 7 -8 9];
>> x(x<0) = 0
x =
1 0 3 0 5 0 7 0 9
% 第2行赋值为0
y =
1 2 3
-4 5 6
7 8 9
>> y(2,:)=0
y =
1 2 3
0 0 0
7 8 9
% 先找到第一列中小于0的,再把那一行都设为0
>> y = [1 2 3;-4 5 6;7 8 9]
y =
1 2 3
-4 5 6
7 8 9
>> y(y(:,1)<0,:)=0
y =
1 2 3
0 0 0
7 8 9
数组操作函数
flipud():行逆序排列
fliplr():列逆序排列
rot90():逆时针90°旋转
>> A = [1 2 3;4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> B = flipud(A)
B =
7 8 9
4 5 6
1 2 3
>> C = fliplr(A)
C =
3 2 1
6 5 4
9 8 7
>> D = rot90(A)
D =
3 6 9
2 5 8
1 4 7
sum():求和函数
>> A = [1 2 3];
>> sum(A)
ans =
6
>> B = [1 2 3;4 5 6;7 8 9];
>> sum(B) % 相当于sum(B,1),每列求和
ans =
12 15 18
>> sum(B,2) % 每行求和
ans =
6
15
24
>> sum(B(:)) % 所有总和
ans =
45
>> C = B(:) % 将B矩阵拉成1维向量
C =
1
4
7
2
5
8
3
6
9
>> A = [1 2 3];
>> max(A)
ans =
3
>> max(A,2) % 跟2比较,取最大
ans =
2 2 3
>> B = [1 3 9;4 8 6]; % 2维数组取最大,默认取每列最大
>> max(B)
ans =
4 8 9
>> max(B,[],2) % 按照行取最大值的格式
ans =
9
8
常用数学函数
sin,cos,tan,cot,asin,acos,atan,acot
>> x = 0:pi/6:pi
x =
0 0.5236 1.0472 1.5708 2.0944 2.6180 3.1416
>> y = sin(x)
y =
0 0.5000 0.8660 1.0000 0.8660 0.5000 0.0000
abs():取绝对值
sqrt():开根号
ceil():向上取整
floor():向下取整
fix():向0靠取整
round():四舍五入取整
mod():取余
简单作图
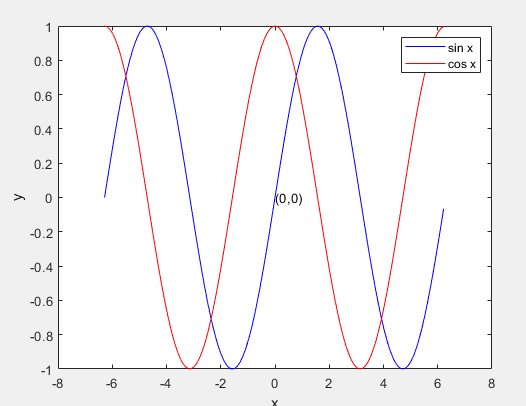
>> x = -2*pi:0.1:2*pi;
>> y1 = sin(x);
>> y2 = cos(x);
>> plot(x,y1,'-b'); % 蓝色实线
>> hold on; % 避免下面的图覆盖掉上面的
>> plot(x,y2,'-r');
>> xlabel('x');
>> ylabel('y');
>> text(0,0,'(0,0)');
>> legend('sin x','cos x');
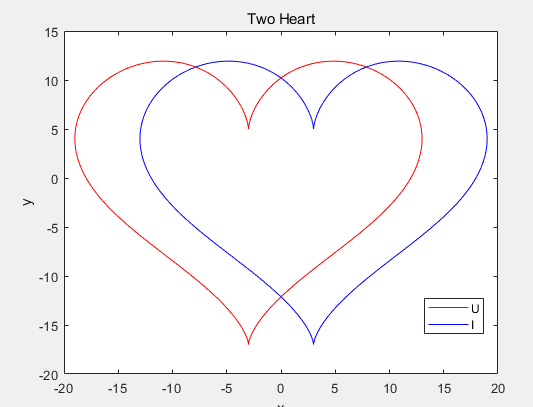
>> t = 0:pi/180:4*pi;
x = 16*sin(t).^3;
y = 13*cos(t)-5*cos(2*t)...
-2*cos(3*t)-cos(4*t);
plot(x-3,y,'-r',x+3,y,'-b');
xlabel('x');
ylabel('y');
>> axis([-20,20,-20,15]); % X、Y轴范围分别是[-20,20]、[-20、15]
>> title('Two Heart');;
>> legend('U','I');
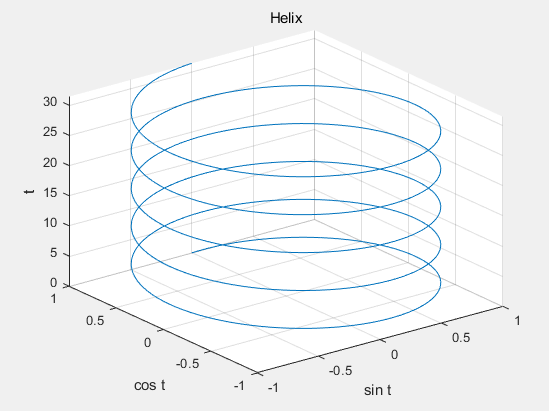
3维作图
>> t = 0:pi/50:10*pi;
x = sin(t);
y = cos(t);
z = t;
>> plot3(x,y,z); % 3维作图
>> title('Helix');
>> xlabel('sin t');
>> ylabel('cos t');
>> zlabel('t');
>> grid on; % 加网格线
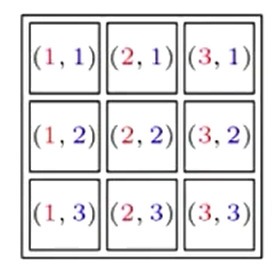
meshgrid():生成格网采样点
>> [x,y] = meshgrid(1:3,1:3)
x =
1 2 3
1 2 3
1 2 3
y =
1 1 1
2 2 2
3 3 3
% 下图为此函数生成的格网点
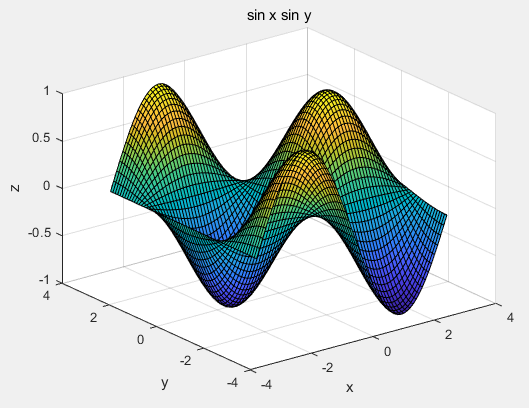
>> [x,y] = meshgrid(-pi:0.1:pi);
>> z = sin(x).*cos(y);
>> mesh(x,y,z); % 绘制3维曲面
>> surf(x,y,z); % 3维着色
>> xlabel('x');
>> ylabel('y');
>> zlabel('z');
>> title('sin x sin y');
M函数格式
% 求矩形面积
function area = rectarea(L,W)
area = L.*W